Czjzek distribution Model¶
- class mrsimulator.models.CzjzekDistribution(sigma: float, polar=False)¶
Bases:
AbstractDistributionA Czjzek distribution model class.
The Czjzek distribution model is a random sampling of second-rank traceless symmetric tensors whose explicit matrix form follows
(78)¶\[\begin{split}{\bf S} = \left[ \begin{array}{l l l} \sqrt{3} U_5 - U_1 & \sqrt{3} U_4 & \sqrt{3} U_2 \\ \sqrt{3} U_4 & -\sqrt{3} U_5 - U_1 & \sqrt{3} U_3 \\ \sqrt{3} U_2 & \sqrt{3} U_3 & 2 U_1 \end{array} \right],\end{split}\]where the components, \(U_i\), are randomly drawn from a five-dimensional multivariate normal distribution. Each component, \(U_i\), is a dimension of the five-dimensional uncorrelated multivariate normal distribution with the mean of \(<U_i>=0\) and the variance \(<U_iU_i>=\sigma^2\).
(79)¶\[S_T = S_C(\sigma),\]- Parameters:
sigma (float) – The Gaussian standard deviation.
Note
In the original Czjzek paper, the parameter \(\sigma\) is given as two times the standard deviation of the multi-variate normal distribution used here.
Example
>>> from mrsimulator.models import CzjzekDistribution >>> cz_model = CzjzekDistribution(0.5)
- pdf(pos, size: int = 400000)¶
Generates a probability distribution function by binning the random variates of length size onto the given grid system.
- Parameters:
pos – A list of coordinates along the two dimensions given as NumPy arrays.
size – The number of random variates drawn in generating the pdf. The default is 400000.
- Returns:
A list of x and y coordinates and the corresponding amplitudes.
Example
>>> import numpy as np >>> cq = np.arange(50) - 25 >>> eta = np.arange(21)/20 >>> Cq_dist, eta_dist, amp = cz_model.pdf(pos=[cq, eta])
- rvs(size: int)¶
Draw random variates of length size from the distribution.
- Parameters:
size – The number of random points to draw.
- Returns:
A list of two NumPy array, where the first and the second array are the anisotropic/quadrupolar coupling constant and asymmetry parameter, respectively.
Example
>>> Cq_dist, eta_dist = cz_model.rvs(size=1000000)
Mini-gallery using czjzek distributions¶
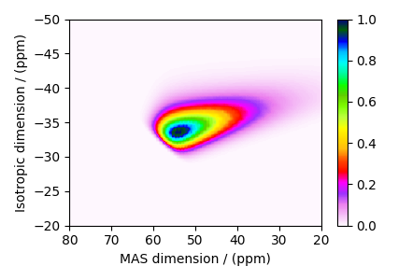
Figure 143 Czjzek distribution, ²⁷Al (I=5/2) 3QMAS¶