RbNO₃, ⁸⁷Rb (I=3/2) 3QMAS¶

⁸⁷Rb (I=3/2) triple-quantum magic-angle spinning (3Q-MAS) simulation.

The following is an example of the 3QMAS simulation of \(\text{RbNO}_3\), which has three distinct \(^{87}\text{Rb}\) sites. The \(^{87}\text{Rb}\) tensor parameters were obtained from Massiot et al. [1]. In this simulation, a Gaussian broadening is applied to the spectrum as a post-simulation step.

import matplotlib.pyplot as plt

from mrsimulator import Simulator, SpinSystem, Site
from mrsimulator.method.lib import ThreeQ_VAS
from mrsimulator import signal_processor as sp
from mrsimulator.spin_system.tensors import SymmetricTensor
from mrsimulator.method import SpectralDimension

Generate the site and spin system objects.

Rb87_1 = Site(
    isotope="87Rb",
    isotropic_chemical_shift=-27.4,  # in ppm
    quadrupolar=SymmetricTensor(Cq=1.68e6, eta=0.2),  # Cq is in Hz
)
Rb87_2 = Site(
    isotope="87Rb",
    isotropic_chemical_shift=-28.5,  # in ppm
    quadrupolar=SymmetricTensor(Cq=1.94e6, eta=1.0),  # Cq is in Hz
)
Rb87_3 = Site(
    isotope="87Rb",
    isotropic_chemical_shift=-31.3,  # in ppm
    quadrupolar=SymmetricTensor(Cq=1.72e6, eta=0.5),  # Cq is in Hz
)

sites = [Rb87_1, Rb87_2, Rb87_3]  # all sites
spin_systems = [SpinSystem(sites=[s]) for s in sites]

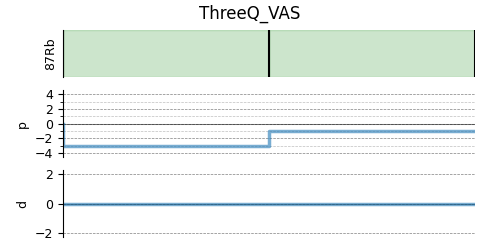
Select a Triple Quantum variable-angle spinning method. You may optionally provide a rotor_angle to the method. The default rotor_angle is the magic-angle.

method = ThreeQ_VAS(
    channels=["87Rb"],
    magnetic_flux_density=9.4,  # in T
    spectral_dimensions=[
        SpectralDimension(
            count=128,
            spectral_width=7e3,  # in Hz
            reference_offset=-7e3,  # in Hz
            label="Isotropic dimension",
        ),
        SpectralDimension(
            count=256,
            spectral_width=1e4,  # in Hz
            reference_offset=-4e3,  # in Hz
            label="MAS dimension",
        ),
    ],
)

# A graphical representation of the method object.
plt.figure(figsize=(5, 2.5))
method.plot()
plt.show()

Create the Simulator object, add the method and spin system objects, and run the simulation.

sim = Simulator(spin_systems=spin_systems, methods=[method])
sim.run()

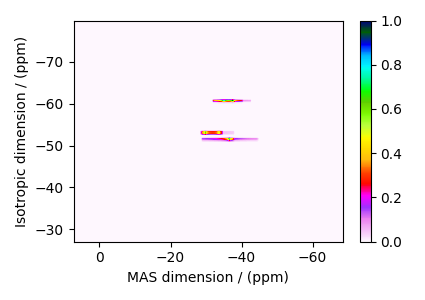
The plot of the simulation.

dataset = sim.methods[0].simulation

plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
cb = ax.imshow(dataset.real / dataset.real.max(), aspect="auto", cmap="gist_ncar_r")
plt.colorbar(cb)
ax.invert_xaxis()
ax.invert_yaxis()
plt.tight_layout()
plt.show()

Add post-simulation signal processing.

processor = sp.SignalProcessor(
    operations=[
        # Gaussian convolution along both dimensions.
        sp.IFFT(dim_index=(0, 1)),
        sp.apodization.Gaussian(FWHM="0.08 kHz", dim_index=0),
        sp.apodization.Gaussian(FWHM="0.22 kHz", dim_index=1),
        sp.FFT(dim_index=(0, 1)),
    ]
)
processed_dataset = processor.apply_operations(dataset=sim.methods[0].simulation)
processed_dataset /= processed_dataset.max()

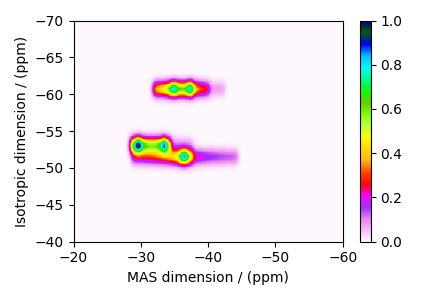
The plot of the simulation after signal processing.

plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
cb = ax.imshow(processed_dataset.real, cmap="gist_ncar_r", aspect="auto")
plt.colorbar(cb)
ax.set_ylim(-40, -70)
ax.set_xlim(-20, -60)
plt.tight_layout()
plt.show()