Note
Go to the end to download the full example code
Simulating site disorder (crystalline)¶
⁸⁷Rb (I=3/2) 3QMAS simulation with site disorder.
The following example illustrates an NMR simulation of a crystalline solid with site disorders. We model such disorders with Extended Czjzek distribution. The following case study shows an \(^{87}\text{Rb}\) 3QMAS simulation of RbNO3.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from mrsimulator import Simulator
from mrsimulator.method.lib import ThreeQ_VAS
from mrsimulator.models import ExtCzjzekDistribution
from mrsimulator.utils.collection import single_site_system_generator
from mrsimulator.method import SpectralDimension
Generate probability distribution¶
Create three extended Czjzek distributions for the three sites in RbNO3 about their respective mean tensors.
# The range of isotropic chemical shifts, the quadrupolar coupling constant, and
# asymmetry parameters used in generating a 3D grid.
iso_r = np.arange(101) / 6.5 - 35 # in ppm
Cq_r = np.arange(100) / 100 + 1.25 # in MHz
eta_r = np.arange(11) / 10
# The 3D mesh grid over which the distribution amplitudes are evaluated.
iso, Cq, eta = np.meshgrid(iso_r, Cq_r, eta_r, indexing="ij")
def get_prob_dist(iso, Cq, eta, eps, cov):
pdf = 0
for i in range(len(iso)):
# The 2D amplitudes for Cq and eta is sampled from the extended Czjzek model.
avg_tensor = {"Cq": Cq[i], "eta": eta[i]}
_, _, amp = ExtCzjzekDistribution(avg_tensor, eps=eps[i]).pdf(pos=[Cq_r, eta_r])
# The 1D amplitudes for isotropic chemical shifts is sampled as a Gaussian.
iso_amp = multivariate_normal(mean=iso[i], cov=[cov[i]]).pdf(iso_r)
# The 3D amplitude grid is generated as an uncorrelated distribution of the
# above two distribution, which is the product of the two distributions.
pdf_t = np.repeat(amp, iso_r.size).reshape(eta_r.size, Cq_r.size, iso_r.size)
pdf_t *= iso_amp
pdf += pdf_t
return pdf
iso_0 = [-27.4, -28.5, -31.3] # isotropic chemical shifts for the three sites in ppm
Cq_0 = [1.68, 1.94, 1.72] # Cq in MHz for the three sites
eta_0 = [0.2, 1, 0.5] # eta for the three sites
eps_0 = [0.02, 0.02, 0.02] # perturbation fractions for extended Czjzek distribution.
var_0 = [0.1, 0.1, 0.1] # variance for the isotropic chemical shifts in ppm^2.
pdf = get_prob_dist(iso_0, Cq_0, eta_0, eps_0, var_0).T
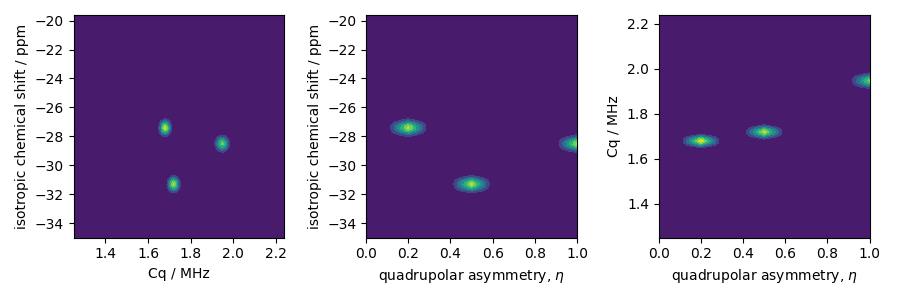
The two-dimensional projections from this three-dimensional distribution are shown below.
_, ax = plt.subplots(1, 3, figsize=(9, 3))
# isotropic shift v.s. quadrupolar coupling constant
ax[0].contourf(Cq_r, iso_r, pdf.sum(axis=2))
ax[0].set_xlabel("Cq / MHz")
ax[0].set_ylabel("isotropic chemical shift / ppm")
# isotropic shift v.s. quadrupolar asymmetry
ax[1].contourf(eta_r, iso_r, pdf.sum(axis=1))
ax[1].set_xlabel(r"quadrupolar asymmetry, $\eta$")
ax[1].set_ylabel("isotropic chemical shift / ppm")
# quadrupolar coupling constant v.s. quadrupolar asymmetry
ax[2].contourf(eta_r, Cq_r, pdf.sum(axis=0))
ax[2].set_xlabel(r"quadrupolar asymmetry, $\eta$")
ax[2].set_ylabel("Cq / MHz")
plt.tight_layout()
plt.show()
Simulation setup¶
Generate spin systems from the above probability distribution.
spin_systems = single_site_system_generator(
isotope="87Rb",
isotropic_chemical_shift=iso,
quadrupolar={"Cq": Cq * 1e6, "eta": eta}, # Cq in Hz
abundance=pdf,
)
len(spin_systems)
509
Simulate a \(^{27}\text{Al}\) 3Q-MAS spectrum by using the ThreeQ_MAS method.
method = ThreeQ_VAS(
channels=["87Rb"],
magnetic_flux_density=9.4, # in T
rotor_angle=54.735 * np.pi / 180,
spectral_dimensions=[
SpectralDimension(
count=96,
spectral_width=7e3, # in Hz
reference_offset=-7e3, # in Hz
label="Isotropic dimension",
),
SpectralDimension(
count=256,
spectral_width=1e4, # in Hz
reference_offset=-4e3, # in Hz
label="MAS dimension",
),
],
)
Create the simulator object, add the spin systems and method, and run the simulation.
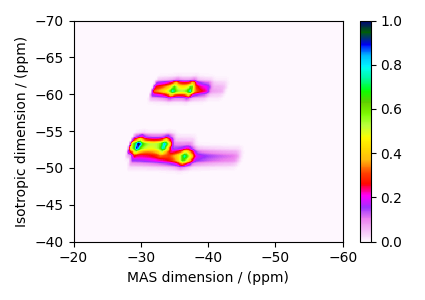
The plot of the corresponding spectrum.
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
cb = ax.imshow(dataset / dataset.max(), cmap="gist_ncar_r", aspect="auto")
ax.set_ylim(-40, -70)
ax.set_xlim(-20, -60)
plt.colorbar(cb)
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 16.447 seconds)
