Extended Czjzek distribution Model¶
- class mrsimulator.models.ExtCzjzekDistribution(symmetric_tensor: SymmetricTensor, eps: float, mean_isotropic_chemical_shift: float = 0.0, abundance: float = 100.0, polar=False, cache=True)¶
Bases:
AbstractDistributionAn extended Czjzek distribution distribution model.
The extended Czjzek random distribution [1] model is an extension of the Czjzek model, given as
(84)¶\[S_T = S(0) + \rho S_C(\sigma=1),\]where \(S_T\) is the total tensor, \(S(0)\) is the dominant tensor, \(S_C(\sigma=1)\) is the Czjzek random model attributing to the random perturbation of the tensor about the dominant tensor, \(S(0)\), and \(\rho\) is the size of the perturbation. Note, in the above equation, the \(\sigma\) parameter from the Czjzek random model, \(S_C\), has no meaning and is set to one. The factor, \(\rho\), is defined as
(85)¶\[\rho = \frac{||S(0)|| \epsilon}{\sqrt{30}},\]where \(\|S(0)\|\) is the 2-norm of the dominant tensor, and \(\epsilon\) is a fraction.
- Parameters:
symmetric_tensor (SymmetricTensor) – A shielding or quadrupolar symmetric tensor or equivalent dict object.
eps (float) – A fraction determining the extent of perturbation.
Example
>>> from mrsimulator.models import ExtCzjzekDistribution >>> S0 = {"Cq": 1e6, "eta": 0.3} >>> ext_cz_model = ExtCzjzekDistribution(S0, eps=0.35)
- add_lmfit_params(params, i)¶
Create lmfit params for index i
- pack_csdm_object(pos, data)¶
Pack data and coordinates as csdm objects
- pdf(pos, size: int = 400000, analytical: bool = True, pack_as_csdm: bool = False)¶
Generates a probability distribution function by binning the random variates of length size onto the given grid system.
- Parameters:
pos – A list of coordinates along the two dimensions given as NumPy arrays.
size – The number of random variates drawn in generating the pdf. The default is 400000.
pack_as_csdm – If true, returns as csdm object.
- Returns:
A list of x and y coordinates and the corresponding amplitudes if not packed as csdm object, else a csdm object.
Example
>>> import numpy as np >>> cq = np.arange(50) - 25 >>> eta = np.arange(21)/20 >>> amp = cz_model.pdf(pos=[cq, eta]) # returns amp as a CSDM object.
- pdf_numerical(pos, size: int = 400000)¶
Generate distribution numerically
- rvs(size: int)¶
Draw random variates of length size from the distribution.
- Parameters:
size – The number of random points to draw.
- Returns:
A list of two NumPy array, where the first and the second array are the anisotropic/quadrupolar coupling constant and asymmetry parameter, respectively.
Example
>>> Cq_dist, eta_dist = ext_cz_model.rvs(size=1000000)
- update_lmfit_params(params, i)¶
Create lmfit params for index i
Mini-gallery using extended czjzek distributions¶
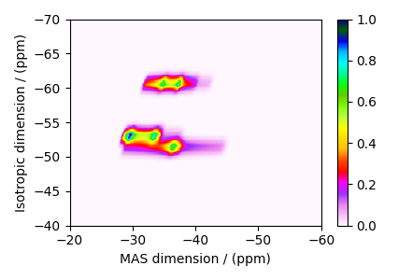
Extended Czjzek distribution (Shielding and Quadrupolar)
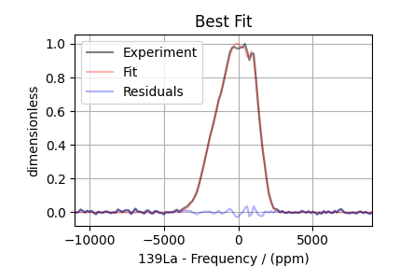
Extended Czjzek fitting of ¹³⁹La MAS NMR of La₀.₂Y₁.₈Si₂2O₇