Note
Go to the end to download the full example code
⁸⁷Rb 2D 3QMAS NMR of RbNO₃¶
The following is a 3QMAS fitting example for \(\text{RbNO}_3\). The dataset was acquired and shared by Brendan Wilson.
import numpy as np
import csdmpy as cp
import matplotlib.pyplot as plt
from lmfit import Minimizer
from mrsimulator import Simulator
from mrsimulator.method.lib import ThreeQ_VAS
from mrsimulator import signal_processor as sp
from mrsimulator.utils import spectral_fitting as sf
from mrsimulator.utils import get_spectral_dimensions
from mrsimulator.utils.collection import single_site_system_generator
Import the dataset¶
filename = "https://ssnmr.org/sites/default/files/mrsimulator/RbNO3_MQMAS.csdf"
experiment = cp.load(filename)
# For spectral fitting, we only focus on the real part of the complex dataset
experiment = experiment.real
# Convert the coordinates along each dimension from Hz to ppm.
_ = [item.to("ppm", "nmr_frequency_ratio") for item in experiment.dimensions]
# plot of the dataset.
max_amp = experiment.max()
levels = (np.arange(24) + 1) * max_amp / 25 # contours are drawn at these levels.
options = dict(levels=levels, alpha=0.75, linewidths=0.5) # plot options
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
ax.contour(experiment, colors="k", **options)
ax.set_xlim(-20, -50)
ax.set_ylim(-45, -65)
plt.grid()
plt.tight_layout()
plt.show()
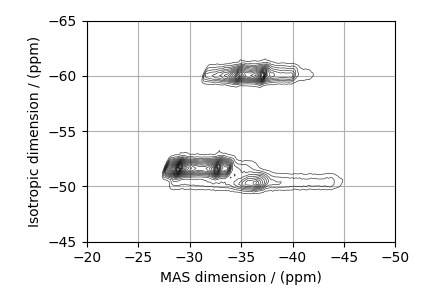
Estimate noise statistics from the dataset.
noise_region = np.where(experiment.dimensions[0].coordinates > -25e-6)
noise_data = experiment[noise_region]
plt.figure(figsize=(3.75, 2.5))
ax = plt.subplot(projection="csdm")
ax.imshow(noise_data, aspect="auto", interpolation="none")
plt.title("Noise section")
plt.axis("off")
plt.tight_layout()
plt.show()
noise_mean, sigma = noise_data.mean(), noise_data.std()
noise_mean, sigma
(<Quantity 1.1995176>, <Quantity 159.38718>)
Create a fitting model¶
Guess model
Create a guess list of spin systems.
shifts = [-26.8, -28.4, -31.2] # in ppm
Cq = [1.7e6, 2.0e6, 1.7e6] # in Hz
eta = [0.2, 0.95, 0.6]
abundance = [40.0, 25.0, 35.0] # in %
spin_systems = single_site_system_generator(
isotope="87Rb",
isotropic_chemical_shift=shifts,
quadrupolar={"Cq": Cq, "eta": eta},
abundance=abundance,
)
Method
Create the 3QMAS method.
# Get the spectral dimension parameters from the experiment.
spectral_dims = get_spectral_dimensions(experiment)
MQMAS = ThreeQ_VAS(
channels=["87Rb"],
magnetic_flux_density=9.395, # in T
spectral_dimensions=spectral_dims,
experiment=experiment, # add the measurement to the method.
)
Guess Spectrum
# Simulation
# ----------
sim = Simulator(spin_systems=spin_systems, methods=[MQMAS])
sim.config.number_of_sidebands = 1
sim.run()
# Post Simulation Processing
# --------------------------
processor = sp.SignalProcessor(
operations=[
# Gaussian convolution along both dimensions.
sp.IFFT(dim_index=(0, 1)),
sp.apodization.Gaussian(FWHM="0.08 kHz", dim_index=0),
sp.apodization.Gaussian(FWHM="0.2 kHz", dim_index=1),
sp.FFT(dim_index=(0, 1)),
sp.Scale(factor=2e8),
]
)
processed_dataset = processor.apply_operations(dataset=sim.methods[0].simulation).real
# Plot of the guess Spectrum
# --------------------------
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
ax.contour(experiment, colors="k", **options)
ax.contour(processed_dataset, colors="r", linestyles="--", **options)
ax.set_xlim(-20, -50)
ax.set_ylim(-45, -65)
plt.grid()
plt.tight_layout()
plt.show()
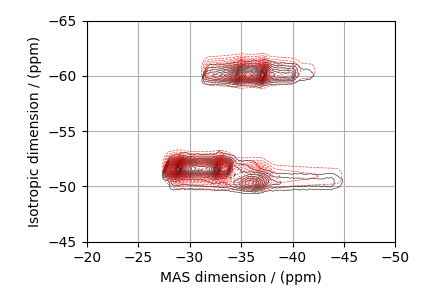
Least-squares minimization with LMFIT¶
Use the make_LMFIT_params() for a quick
setup of the fitting parameters.
params = sf.make_LMFIT_params(sim, processor)
print(params.pretty_print(columns=["value", "min", "max", "vary", "expr"]))
Name Value Min Max Vary Expr
SP_0_operation_1_Gaussian_FWHM 0.08 -inf inf True None
SP_0_operation_2_Gaussian_FWHM 0.2 -inf inf True None
SP_0_operation_4_Scale_factor 2e+08 -inf inf True None
sys_0_abundance 40 0 100 True None
sys_0_site_0_isotropic_chemical_shift -26.8 -inf inf True None
sys_0_site_0_quadrupolar_Cq 1.7e+06 -inf inf True None
sys_0_site_0_quadrupolar_eta 0.2 0 1 True None
sys_1_abundance 25 0 100 True None
sys_1_site_0_isotropic_chemical_shift -28.4 -inf inf True None
sys_1_site_0_quadrupolar_Cq 2e+06 -inf inf True None
sys_1_site_0_quadrupolar_eta 0.95 0 1 True None
sys_2_abundance 35 0 100 False 100-sys_0_abundance-sys_1_abundance
sys_2_site_0_isotropic_chemical_shift -31.2 -inf inf True None
sys_2_site_0_quadrupolar_Cq 1.7e+06 -inf inf True None
sys_2_site_0_quadrupolar_eta 0.6 0 1 True None
None
Solve the minimizer using LMFIT
opt = sim.optimize() # Pre-compute transition pathways
minner = Minimizer(
sf.LMFIT_min_function,
params,
fcn_args=(sim, processor, sigma),
fcn_kws={"opt": opt},
)
result = minner.minimize()
result
The best fit solution¶
best_fit = sf.bestfit(sim, processor)[0].real
# Plot the spectrum
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
ax.contour(experiment, colors="k", **options)
ax.contour(best_fit, colors="r", linestyles="--", **options)
ax.set_xlim(-20, -50)
ax.set_ylim(-45, -65)
plt.grid()
plt.tight_layout()
plt.show()
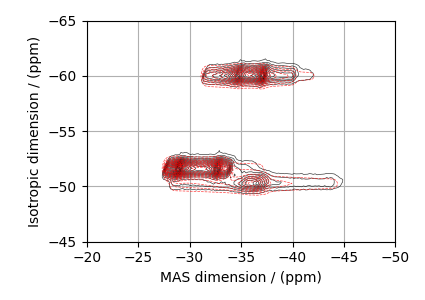
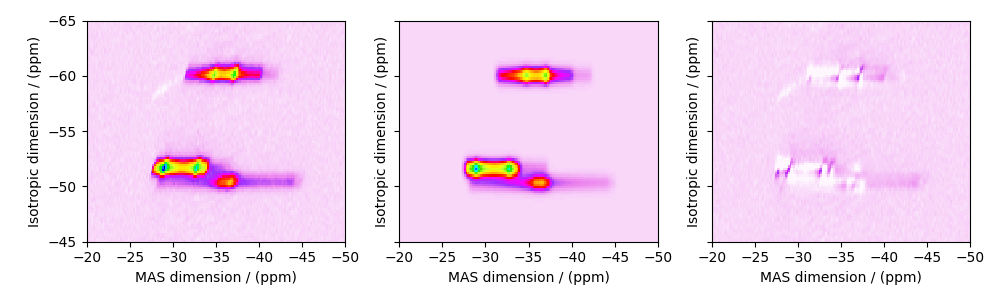
Image plots with residuals¶
residuals = sf.residuals(sim, processor)[0].real
fig, ax = plt.subplots(
1, 3, sharey=True, figsize=(10, 3.0), subplot_kw={"projection": "csdm"}
)
vmax, vmin = experiment.max(), experiment.min()
for i, dat in enumerate([experiment, best_fit, residuals]):
ax[i].imshow(
dat,
aspect="auto",
cmap="gist_ncar_r",
vmax=vmax,
vmin=vmin,
interpolation="none",
)
ax[i].set_xlim(-20, -50)
ax[0].set_ylim(-45, -65)
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 16.006 seconds)
